고정 헤더 영역
상세 컨텐츠
본문
안녕하세요. 수업을 기록하는 수학쌤입니다. :)
벚꽃과 함께 4월 첫 주가 훌쩍 지나갔네요.
날씨가 좋아지는만큼 싱숭생숭한 분위기에서도 수학 수업은 계속될테고요 ㅎㅎ
특히나 금요일이라 더욱 설레는 오늘 !
일주일을 잘 마무리하기 위해 오늘의 수업 기록 역시 시작해보겠습니다^_^
I. 수와 연산 - 2. 정수와 유리수 - 01. 정수와 유리수 - 3. 직선 위에 수 나타내기
1. 이번 차시에 대한 초안
지난 시간에 정수와 유리수를 배우며 자연수에서 한 단계 더 나아간 아이들인데요,
이 수 체계를 정확하게 이해 기억하고 있는지 이번 시간에는 모둠 활동을 먼저 진행하며 복습 시간을 가진 후
새로운 진도를 나가보려고 해요.
그렇기에, 진도를 나가는 데 들이는 시간은 평소보다 적게 사용을 했고 학습지도 간결하게
1쪽으로 구성했어요.
2. 학습지 구성과 수업 진행

평소보다 학습지에 구성된 학습량이 적으니
아이들도 자연스레 기대를 하더라고요.
오늘 수업 일찍 끝날 거라면서요. ㅎ
일단은 간단하게
[복습] 교과서 문제 해결하기를 스스로 해보도록 합니다.
그리고 다함께 해결하며 지난 시간에 배운 내용을 떠올려보는 시간을 갖고요,
[모둠활동] 에서 PPT를 이용하여 카드 뒤집기 놀이를 해보았어요.
이때 이용한 PPT는 제가 신규 때부터 수업 준비를 할 때 잘 이용한 네이버 카페인
'학생과 선생님 모두가 즐거운 수학 수업'에서 다운받은 자료입니다.
일단 규칙을 먼저 설명해주고 PPT를 켰어요.

이 화면이 첫 화면입니다.
규칙 1. 선생님이 보여주시는 PPT 화면을 5초간 잘 본다.
이에 따라 다음의 화면으로 넘어가면

이처럼 앞 슬라이드의 카드를 뒤집은 화면이 나와요.
카드는 다양한 종류의 수로 채워져있죠.
5초가 지나면 다시 첫 화면으로 돌아가도록 슬라이드쇼가 진행이 돼요.

그럼 이제 여기서 다음 규칙 적용 !
규칙 2. 선생님이 제시하시는 조건에 맞는 수를 모둠원마다 1개씩 이야기한다.
이때, 속도가 생명이다! 모둠원 한 명이 틀리는 순간 다른 모둠으로 pass!
이말이 무슨 말이냐면
화면 2에서 유심히 본 숫자들이 어느 알파벳 카드 뒤에 적혀있는 수인지를 기억했다가
교사가 제시하는 수, 예를 들어 '음의 정수'를 제시한다면
음의 정수가 적혀있는 것으로 기억이 된 알파벳을 얘기하는거죠.
모둠 활동이라서 모둠별로 한명씩만 지정하여 우리 모둠이 발표하겠다는 의사를 표명할 수 있도록
손을 들게 하고,
제 기준 가장 빨리 손을 든 친구의 모둠에 기회를 주면
그 모둠원(보통 4명, 많으면 5명) 각각이 이 수에 해당되는 수가 적힌 것으로 기억이 되는
알파벳을 외치는 겁니다.
물론 앞 친구가 외친 건 당연히 외치면 안 되겠고, 속도도 빨라야합니다.
모둠원 1이 S를 외쳤다면
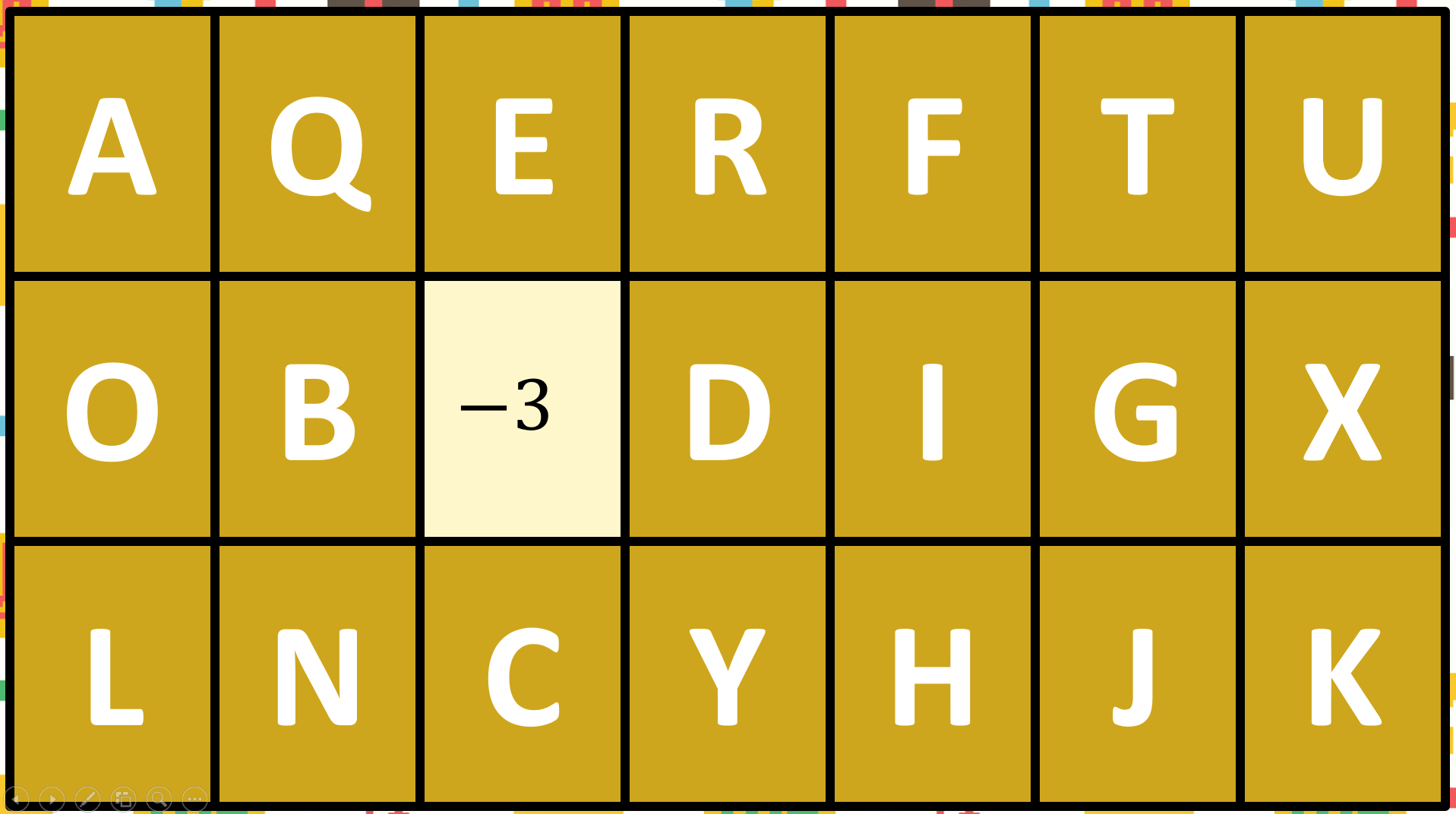
제가 S를 뒤집어 보이고, 제시한 수 체계에 맞는 수라면
다음 모둠원에게 기회가 돌아가고요,
그 다음 모둠원이 D를 외쳤다면

D를 펼쳐보이는데 이때 나온 수가 해당되는 수가 아니라면
그 모둠은 탈락하게 되는 겁니다.
당연히....ㅎ
첫 판엔 이런 게임인 줄 몰랐을테니 모두 카드를 유심히 보지 않아서
순식간에 까먹기 때문에 전원 탈락을 하게 되고요,
한판만 진행을 해도 이제는 어떤 게임인지 감이 왔으니깐 매의 눈으로 모든 카드를 뒤집었을 때의 화면을 잘 살펴봅니다.
두번째 판부터는 아주 살벌하고 흥미진진한 게임이 되는데요, ㅎ
일단 모두가 선착순으로 말하려고 손을 열심히 들고
앞 모둠에서 한명이라도 실수를 하게 되면
다음 모둠에게는 자연스레 앞 모둠에서 성공한 모둠원들이 뒤집은 카드가 정보가 되기 때문에
성공할 확률이 더 높아지게 되죠.
이렇게 하다보면 성공한 모둠들이 생깁니다.
제가 딱히 간식을 준다거나 그 어떤 보상을 제시하지 않아도
그냥 승리라는 목표 하나만 보고 매우 열심히 게임에 참여를 하더라고요.
그래서 제가 5판 정도만 하고 이제 그만 하자고 하면
한판만 더 하자고 하기도 하고요,,,ㅋㅋ
교사가 제시하는 수에는 아무 제한이 없기 때문에
저는 '정수가 아닌 양의 유리수' 이와 같은 수도 계속적으로 얘기했어요.
아이들이 엄청나게 집중하고 이에 해당하는 수를 찾아내려는 노력이 돋보이는
즐거운 모둠 활동이었습니다.
이제 실컷 놀았으니 오늘의 새로운 진도를 나갈 차례입니다.
앞선 모둠활동이 은근 시간을 잡아먹었고, 아이들에게도 너무 즐거운 여파로 여운을 남겨서
다음 내용을 진행하기가 쉽지는 않았는데,
그래도 아이들이 즐거워하는 모습이 보기 좋아서 뿌듯했답니다.
[탐구] 수를 직선 위에 나타낼 수 있을까?
수를 숫자로만 나타내는 것이 아니라 다른 수단을 이용해서도 표현하는 것을 배울 차례인데
나타내야 할 수의 예시가 필요하니 다음과 같은 단계를 주었습니다.
1. 지금까지 배운 정수와 유리수 중 6개의 수를 아래 ☐안에 써보자. (단, 양의 정수와 음의 정수, 양수, 음수가 모두 포함되도록 쓴다.)

괄호 안의 조건을 충족시켜서 해당되는 수를 모두 썼는지 짝꿍과 서로의 수를 검토해보는 시간도 가져보고요~
2. 위에서 쓴 숫자 6개를 자기 나름의 방법으로 아래 직선 위에 표시해보자.

직선을 하나 그려주고 자신의 수를 자기 나름의 방법으로 직선 위에 표시하게 했어요.
어떤 방식을 생각해낸건지 발표하게 했는데 은근 다양한 답변이 나왔습니다.
그 중 가장 많이 나온 이야기로는 '숫자 0을 기준으로 해서 표현한다'였는데
숫자 0을 가장 왼쪽에 쓴 친구들도 있더라구요?
이 경우 음의 정수나 음수는 어떻게 표현할 거냐고 했더니 아! 하면서 답변을 수정하는 친구들도 있었고요.
일단 발표하는 친구들 중에서는 숫자 0이 양수와 음수를 구분하게 하는 기준이 되니깐
0을 직선 위의 적당한 중간 지점에 쓰고
그 양쪽으로 양수와 음수를 배치한다고 답하는 경우가 많았습니다.
물론, 편견 없이 양수를 0의 왼쪽에, 음수를 0의 오른쪽에 쓴다는 답변도 있었고요.
우리는 아직 아무 것도 배우지 않은 상황이기 때문에 이러한 답변도 긍정적으로 바라보며 칭찬해주었어요.
3. +5와 –5는 각각 어떻게 직선 위에 표시할 수 있을까? 자신의 생각을 적어보자.
이 경우 (+) 부호와 (-) 부호 뒤에 붙어있는 수가 같기 때문에 뭔가 표현하는 방식을 비슷하지만
분명한 차이는 있어야하죠.
이에 대해 어떤 차이를 줄 것인지 생각해보게 하고 싶어서 준비한 문항이었고요,
발표에 참여한 친구들의 경우
0을 기준으로 양쪽에 같은 개수의 점을 찍되 이웃한 점끼리의 거리가 모두 같도록 찍는다고 설명을 시작했습니다.
그리고 이웃한 점 사이의 거리를 1이라고 생각하면
0으로부터 한쪽 방향으로 5만큼 이동한 곳에 +5를,
반대쪽 방향으로 5만큼 이동한 곳에 -5를 적었다고 하더라고요.
이동하는 거리는 같지만 이동하는 방향은 반대로 표현함으로써
+5와 -5의 공통점과 차이점을 잘 나타냈어요.
발표를 들을 때까지는 아무 것도 지정해주지 않았어요. 방향도, 용어도요.
4. 1/2과 -(5/4)는 각각 어떻게 직선 위에 표시할 수 있을까? 자신의 생각을 적어보자.
이 문항은 정수가 아닌 유리수는 어떻게 직선 위에 나타내면 좋을지 생각해보게 하고 싶어서
구성했는데요,
발표한 친구들은 곧잘 답하더라고요.
대신 중학교에 근무한 이래로 정말 오래만에 용어 하나를 들었습니다.
바로 가분수와 대분수였는데요..ㅋㅋ
-(5/4)의 경우 5/4가 가분수이기 때문에
대분수인 1(1/4)로 바꿔야한다고 하는데... 너무 맞는 말인데
그냥 귀여웠습니다..ㅋㅋ
1/2을 나타내는 점은
0을 나타내는 점과 1을 나타내는 점 사이의 거리를 분모인 2를 이용하여 2등분한 후
그 중 한 칸만 이동하면 되고,
-(5/4) = -1(1/4)의 경우 1/2의 위치를 찾기 위해 이동한 방향과 반대 방향을 택하여
1칸을 먼저 이동하고 이동한 점에서 시작하여 그 다음 점과의 거리를
분모인 4를 이용하여 4등분한 후,
분자에 해당하는 1만큼 추가로 이동하면 된다고 발표 또는 저의 설명이 마무리가 됐어요.
여기까지 준비한 문항들이 의도하는 바는
- 위의 수들은 직선 위에 항상 나타낼 수 있다.
- 직선 위에 기준점을 잡고 그 점으로부터 서로 다른 방향으로 이동한다면 부호가 다른 수도 나타낼 수 있다.
였어요. 일단 이 사실을 언급하며 아이들이 이해하도록 합니다.
위의 문항들을 해결하는 과정에서 이 사실들이 이해는 될거라 좀더 정돈된 언어로 표현할 필요가 있었습니다
그렇기에 용어를 정리하고, 수학에서 약속한 사실들을 소개해야해요.
직선 위에 점 O를 잡고 그 점에 수 0을 대응시킨다.점 O의 좌우에 일정한 간격으로 점을 잡고,
점 O의 오른쪽 점에는 양수를,
점 O의 왼쪽 점에는 음수를 차례로 대응시킨다.
이와 같이 수를 대응시킨 직선을 수직선이라 하고,
O를 원점이라고 한다.
이처럼 정리하면
정수, 유리수는 항상 직선 위에 나타낼 수 있다는 사실과 함께
어떻게 나타낼 수 있는지,
이 직선의 이름,
기준이 되는 점인 원점에 대해서도 빠짐없이 설명하게 된 셈입니다.
앞으로 매우 익숙하게 사용할 수직선이지만
그 배경과 약속부터 정확히 익히게 됐으니 기초를 탄탄하게 다졌다고 볼 수 있겠죠 ?
마지막 OX 퀴즈와 함께 이번 시간을 마무리했어요.
1) 모든 유리수는 수직선 위의 점에 대응시킬 수 있다. (O/X)
-> 위의 문항 4에서 한번 다루었으니 O라고 답할 수 있어요.
2) 수직선 위의 한 점에 해당하는 유리수를 항상 찾을 수 있다. (O/X)
-> 이 부분은 사실 중 1 교육과정에서 설명할 수는 없긴 한데... 그렇기에 아니라고만 했습니다.
아닌 예시는 2, 3학년 때 배운다고 말이죠. ㅎ
이 문항은 사실 수업 준비하면서도 넣을지 뺄지 고민했는데 그래도 1) 문항의 역을 한번쯤은 제시해보고 싶었어요.
이렇게 이번 시간의 수업은 끝 !
3. 수업 성찰
복습 모둠 활동에서 활기찬 시간을 보냈고
오늘의 새로운 수업 내용도 사실 아이들에겐
너무 깊게 들어가지 않는한 익숙한 부분이라
수업이 전반적으로 밝은 에너지를 갖추고 있었어요.
떠들 기회도 많고 자신의 의견을 표출할 시간도 많은 수업이었기에
보다 가볍게 진행된 느낌이었고요.
그래서 저에게도 여러모로 즐겁게 진행된 수업이라고 느껴진 시간이었습니다.
다음 시간에는, 수직선을 이용하여
수의 대소 비교를 해보고 절댓값이라는 용어도 정의를 해보려고 합니다.
다음 수업 기록으로 돌아올게요. :)
'중 1 수학수업 기록' 카테고리의 다른 글
| 중학교 1학년 자유학기 수학 수업, 14차시. 정수와 유리수의 덧셈 (1) | 2024.04.24 |
|---|---|
| 중학교 1학년 자유학기 수학 수업, 13차시. 수의 대소 비교 (0) | 2024.04.22 |
| 중학교 1학년 자유학기 수학 수업, 11차시. 정수와 유리수 (2) | 2024.04.03 |
| 중학교 1학년 자유학기 수학 수업, 10차시. 양의 부호와 음의 부호 (0) | 2024.03.30 |
| 중학교 1학년 자유학기 수학 수업, 8차시. 최소공배수의 활용 (1) | 2024.03.26 |




